Частину понять з-посеред тих, які вважають невизначеними, запропоновано називати українською терміном «неясні» (vague predicates) [1], щоб відмежувати їх від інших видів невизначеності. Згадані поняття можна здефініювати як такі, межі яких із суміжними поняттями є кількісно чи якісно невизначеними. Унаслідок розмитості меж, уживання цих понять у міркуваннях може призводити до виникання сористичних парадоксів (σωρίτης давньогрец. нагромаджений).
Суть згаданих парадоксів полягає в такому. Міркують про об’єкт, який на підставі певного ступеня прояву якоїсь з ознак початково осягали відповідним поняттям. Унаслідок послідовної зміни ступеня прояву цієї ознаки згаданий об’єкт перетворюється на інший. Цей новий об’єкт треба було б осягати суміжним поняттям, якому відповідає набутий унаслідок накопичення послідовних змін ступінь прояву змінюваної ознаки. Однак унаслідок міркувань виcновковують, що цей новий істотно інакший об’єкт і далі треба називати попереднім іменем. Наприклад, парадокс «купа». Нехай маємо початковий об’єкт – одне зернятко. Міркують так: оскільки одне зернятко не можна назвати купою, і, додаючи одне зернятко ми не перетворюємо некупу в купу, то, додаючи по одному довільну велику кількість зерняток (піщинок, чи будь‑яких інших предметів) до початково одного ми ніколи не зможемо отримати купи. Тобто, ми внаслідок послідовного збільшення кількості зернят насправді отримали купу, однак, згідно з висновком у наведеній схемі міркувань, нагромаджений сукуп зернят не є купою. Подібно в зворотному порядку – віднімаючи по зернині чи піщинці від їхньої довільно великої кількості в купі ми не перетворимо купу на некупу навіть тоді, коли з початкової купи лишиться лише одна зернина (піщинка) – адже на жодному з кроків такого віднімання ми не маємо більше підстав, аніж на іншому, для твердження, що вже потому купа перетвориться на некупу.
Початкове аналізування наштовхує на думку, що парадокс є наслідком браку в міркуванні чіткої межі між купою і некупою. Отже, якщо встановити таку межу, то парадокс не виникатиме. Однак, на цьому ґрунті виникає такий поширений спосіб аналізування проблеми [2; с. 159]: до прикладу, хай межею купи є 10 000, тобто 9 999 зернят уже не буде купою; однак відмінність між 10 000 і 9 999 настільки мала, що встановлена межа виглядає неприродною, довільною, волюнтаристською; отже, таке встановлювання сталої межі є некоректним. На підставі цих міркувань роблять висновок – оскільки нема змоги встановити обґрунтовану межу діапазону, яка перетворила б неясне поняття в ясне (бо волюнтаризм у встановленні цієї межі призведе до унеможливлення використання цього поняття), то треба відмовитися від такого шляху розв’язання проблеми й шукати інших підходів. Такі міркування сприяли сформуванню чималої кількості різних способів пояснення суті парадоксу та шляхів його уникання.
Сористичний парадокс можна сформулювати в разі вживання: прикметників які мають ступені порівняння; відповідних їм прислівників; а також займенників та іменників, компонентом змісту яких є визначена чи невизначена кількість або ж інтенсивність прояву ознаки (наприклад, гілля, бадилля, лисий, армія, колектив, група, вечір, гора, багато, небагато, мало, високий, невисокий, низький, швидкісний, далекий, гарячий, червоний тощо). Наприклад [3], горнятко кави за 5 $ – це дорого; якщо горнятко кави коштує на цент менше, аніж дороге горнятко кави, то це дорого; отже, безоплатне горнятко кави – це дорого. Або ж інший приклад: театр на 1000 місць є великим; театр, у якому на одне місце менше, аніж у великому, є великим; отже, театр на 10 місць є великим.
Від 70-х років ХХ ст. зацікавленість дослідників цією проблемою стрімко зросла, у зв’язку з бажанням розробити інструментарій для формального виявляння суперечностей згаданого типу та їхнього недопущення. У зв’язку з цими запитами, актуальним є пошук відповідей на питання: якими мають бути засоби формального виявляння подібних суперечностей, наскільки досконалі дефініції неясних понять, і, чи можна внеможливити несвідоме формування таких парадоксів завдяки уміщуванню в дефініціях інформації щодо умов коректного вживання слів із неясною семантикою.
Велику кількість різних моделей пояснення джерел сористичних суперечностей можна згрупувати в декілька підходів: метафізичний, епістемічний, семантичний, прагматичний. Згідно з прибічниками метафізичного підходу (частина з них аналізує предметну ділянку квантової механіки [4]), причиною наявності понять із семантикою невизначеності є те, що невизначеною є сама дійсність. Уважаю, що цей напрям треба відразу відкинути, оскільки буття не може бути «таким» і «нетаким» водночас.
Епістемісти пояснюють джерело виникнення парадоксу таким чином [5; 6]. Суперечність виникає не через те, що відсутність чітких меж є властивістю дійсності, – чіткі межі існують, однак ми в зв’язку з тими чи тими причинами не можемо знати де проходять ці межі. Як це можна тлумачити? Якщо, для прикладу, комусь треба ідентифікувати чи колір певного предмета є червоним, то, не знаючи, де є межа в плавному переході у спектрі від червоного до суміжних кольорів, можемо сумніватися чи згаданий предмет є червоним, чи ні (тобто, чи колір спостережуваного предмета є відтінком червоного, чи відтінком суміжного діапазону). Навіть знаючи числові значи́ни параметрів, відповідні межам діапазону червоного кольору (довжин хвиль, чи частот, чи енергії фотонів), ми можемо мати труднощі з практичним визначенням цих меж, оскільки не носимо приладів для ідентифікації кольору. Подібні аргументи щодо неможливості знати межі кольорів під час ідентифікування кольору предмета треба відкинути. Справді, переважна більшість не знає числових значи́н параметрів, яким відповідають межі діапазонів того чи того кольору. Однак, ідентифікуючи кольори, ми діємо іншим чином – співставляючи їх зі зразком. Щодо цього механізму ідентифікування кольору також можна формулювати аргумент, що ми не утримуємо в пам’яті відтінків, які є межами діапазонів того чи того тону, тобто не знаємо меж. Але з цього факту не випливає, що людина взагалі не встановлює таких меж, ідентифікуючи кольори. Навпаки, без такого встановлення меж не можна було б уживати назви кольорів – перш ніж назвати щось червоним, треба дати відповідь на питання, чи в межах відтінків червоного є колір сприйманого предмета. Отже, практика вживання нами назв кольорів чи інших слів із семантикою якісної чи кількісної невизначеності спонукає погодитись із тим, що межі невизначеного доконечно встановлюють, називаючи предмети словами з неясною семантикою, тобто згадані межі не можна вважати невідомими, а отже, підхід епістемістів також треба відкинути.
Згідно з прибічниками семантичного підходу до явища неясності [7–10], це явище є наслідком специфіки неясних понять, неясних предикатів, яка полягає в тому, що до змісту цих понять (тобто й до значини́ відповідних слів) не входить і не має входити інформація про межі, якими згадані поняття відрізняються від суміжних неясних понять (велике від невеликого, купа від некупи, один колір від іншого тощо). Щодо цього підходу чинними є ті ж контраргументи, що й щодо попереднього. Справді, перш ніж назвати щось великим чи червоним, чи купою, ми змушені були попередньо встановити межі (між великим і невеликим, між купою і некупою, між червоним, і, до прикладу, помаранчевим). Тож якщо однієї універсальної межі нема, то й інформації про неї нема в семантиці неясних понять, однак (треба заперечити прибічникам цього підходу) це не значить, що такі межі не мають існувати в кожному конкретному випадкові вживання цих слів (відповідно до обставин). Уживаючи неясні слова, установлюють межі з такою точністю, яка дозволяє відрізнити суміжні неясні поняття і «прив’язати» йменований об’єкт до одного з них. Оскільки, згідно з прибічниками семантичного підходу, семантика неясних предикатів не містить точної інформації про межі, то в разі вживання цих предикатів класична логіка стає нечинною, і тому, щоб уникнути суперечностей потрібно розробляти спеціальніий логічний апарат.
Прагматики (контекстуалісти) переконані, що межу встановити можна [3; 11], але не розглядають усі типи предикатів із невизначеною семантикою. Крім того, прагматики не відповідають на питання, чи дає цей підхід змогу уникнути спірних випадків, коли значина покроково змінюваного параметра перебуває на межі.
На підставі виконаного огляду можна стверджувати, що недоліком переважної більшості підходів до аналізування неясних предикатів є віддаленість моделей уживання предикатів із неясною семантикою від практики вживання згаданих предикатів. Зокрема, той факт, що загал уживає слова червоний, купа, лисий, великий тощо, які мають неясну семантику, на позначення предметів й ознак, дає підстави стверджувати, що в процесі вживання цих слів суб’єкти мовлення встановлюють межу, а отже, вона є, і вона відома суб’єктові, який позначає щось згаданими предикатами. Зважаючи на це, потрібно провести дослідження неясних предикатів на підставі аналізу механізмів формування їхніх значи́н суб’єктом мовлення в процесі їхнього вживання для кваліфікування об’єктів позамовної дійсності. Мета цього дослідження виявити й систематизувати механізми формування меж значень неясних предикатів і виявити ту істотну для уникнення суперечностей інформацію, яку доцільно було б уміщувати в дефініціях неясних понять.
Перш ніж перейти до аналізування конкретних неясних предикатів, розділимо їх на дві якісно відмінних групи, відповідно до механізму виникнення сористичної суперечності:
1. Слова, компонентом змісту яких є та ознака, яку покроково змінюють у сористичних міркуваннях (наприклад, компонентом змісту поняття «висока людина» є вертикальний лінійний розмір (зріст) людини, який і змінюють покроково в сористичних міркуваннях).
2. Слова, компонентами змісту яких є не та ознака, яку покроково змінюють, однак покрокові зміни однієї ознаки призводять до зміни іншої, уже істотної для аналізованого поняття ознаки. Наприклад, кількість елементів не є істотною ознакою для поняття «купа»: купа може містити всього лише три елементи, скажімо, коли на двох брусках лежить третій. Водночас, істотною в змісті поняття «купа» є ознака розташування одних її елементів над іншими, тобто згромадженість елементів. Покроково зменшуючи кількість елементів у купі, ми можемо дійтго вигляду цього сукупу предметів, коли їх буде розташовано в одному ряді. У такому разі кількісна зміна (знімання останнього предмета з другого ряду) призведе до втрати сукупом згаданої істотної для називання певного сукупу «купою» ознаки – тоді купа перетвориться на некупу. Щодо поняття «купа», зауважмо, що одним із його значи́н є «велика кількість», «багато» і в цьому разі не йдеться про ознаку згромадженості предметів, однак у однойменному сористичному міркуванні йдеться саме про нагромадження предметів.
Оскільки сористичні міркування, у яких використовують перший із наведених видів неясних предикатів, простіші для аналізування, то розпочнімо дослідження саме з таких предикатів. Насамперед розгляньмо слово з семантикою невизначеної кількості «великий» і з’ясуємо, чи позначають цим словом якусь конкретну межу і якщо так, то яким чином її визначають.
Слово «велике» було б позбавлене значини, якби не існували суміжні до нього слова «невелике» (сюди входять малі й середні розміри предметів) й «середнє». Отже, великим щось є в порівнянні з невеликим, чи в порівнянні двома діапазонами розмірів (мале й середнє). Це означає, що щось є великим завжди в порівнянні з якимось орієнтиром. Розгляньмо види орієнтирів, стосовно яких предмети називають великими:
1. «Велике», як познака того, що внаслідок поділу множини предметів на дві групи (одна з яких має цю ознаку, а друга – ні), лінійні розміри предметів того діапазону, який кваліфікують як «велике», відповідають другій, завершальній частині послідовності чисел. Отже, невеликі предмети характеризуватиме те, що їхні лінійні розміри описує початкова частина діапазону чисел. Таким чином у цьому випадкові орієнтир пов’язано з середньою значиною розмірів у групі.
Розгляньмо ситуацію, коли треба поділити предмети на великі, середні й малі. Нехай треба сортувати на групи огірки за розміром, оскільки подальше кулінарне опрацьовування кожної з цих груп буде різним. Оглянувши розміри всіх огірків сортованого сукупу, ми поділяємо розміри на три рівні діапазони. Потому порівнюємо розмір кожного безпосередньо відображуваного огірка зі сформованим в уяві орієнтиром межі між діапазоном великих і діапазоном середніх. Вислідом такого порівняння є прийняття рішення – куди актуально сприйманий нами огірок маємо додати (до великих чи до середніх). Відповідно до того, що сукуп огірків, які маємо сортувати, у кожному конкретному випадкові буде відрізнятися різним діапазононом чисел, межі між малими й середніми, як і між середніми й великими в кожному випадкові будуть різними. Однак ці межі будуть, суб’єкт пізнання сам їх і встановить. Подібним чином можна скваліфікувати як малих, чи середніх, чи великих тварин певного виду, людей, предмети будь-якого виду.
2. Абсолютний орієнтир як розмір суб’єкта оцінювання (тобто суб’єкт порівнює розмір якогось предмета зі своїм чи чиїмось розміром). Коли купа піску більшої висоти порівняно зі зростом дитини, то для дитини ця купа є великою, тоді як та сама купа для дорослої, вищої людини, буде малою. Застерігаючи дитину (не вилазити на велику купу) дорослий, для якого купа насправді є малою, бере за порівняльний орієнтир зріст дитини.
3. Орієнтиром може бути бажаний ступінь вияву ознаки. Наприклад, коли хтось купує полядвицю і просить продавчиню відкраяти шматок певної довжини, то на її питання «чи такий підходить?» покупець може оцінити його як малий порівняно з бажаним, або великий, або такий, що підходить. Подібно можна висловлювати оцінку щодо того, скільки вам запропонували певного напою чи страви, або оцінити розмір одягу чи меблів під час їхнього моделювання тощо.
Це стосується також певного розміру чогось, що не є суб’єктивно бажаним, але об’єктивно потрібним для певного технологічного процесу. Наприклад, розмір деталі для її з’єднування з якимось іншими конструктивним елементом може бути чітко визначеним, коли він буде більшим чи меншим, його оцінюють як великий чи малий. До цієї групи можуть належати також норми чи розміри, які унормували стандартами, – відхили в той чи той бік буде скваліфіковано як «великі» чи «малі». У цьому разі, джерело орієнтира є зовнішнім щодо суб’єкта, який порівнює.
Щодо описаних механізмів установлювання меж може виникнути низка питань. Наприклад: якщо дитина вважає певну купу великою, а дорослий (високий) – малою, то це маємо тлумачити як суперечність, оскільки один і той самий об’єкт названо несумісними ознаками (ступенями прояву ознак). Ба більше, унаслідок індивідуальних відмінностей і різних зовнішніх чинників, два суб’єкти порівнювання розмірів одного об’єкта можуть установити різну межу, до прикладу, коли хтось вважатиме певний предмет належним до однієї групи розмірів (наприклад, великих), а хтось – до іншої (відповідно, невеликих). Вочевидь, що таких суперечностей уникнути неможливо, і для опису таких суперечностей доцільно використати паранесуперечливу логіку.
Інше питання – до якого діапазону розмірів (великих чи невеликих) належать ті розміри, які перебувають на межі? Розгляньмо процес вимірювання. Домовимось, що предмети, довжина яких менша чи дорівнює 10 см, є невеликими. Отже, 11 – це вже великий розмір. Якими є ті предмети, розмір яких на межі, тобто в межах діапазону між 10 і 11, наприклад, 10,3 см. Відповідь очевидна – розмір треба заокруглити, використовуючи загальноприйняті правила, тобто всі розміри менші чи рівні 10,4 заокруглюватимемо до 10, а розміри, від 10,5, – до 11. Якщо ж виникне сумнів, бо знову розмір припаде на межу між 10,4 і 10,5, то треба ще на порядок підвищити точність і так доти, поки ми не зарахуємо предмет до великого чи малого. Безмежно цей процес тривати не може, оскільки в такому разі треба визнати, що предмет не має фіксованого розміру. (Перебіг цих міркувань спростовує також уявлення, що межа між числами також має свої межі й так до нескінченності). Кількісну межу можна встановити інакше. Нехай межею є 10 см із тим, що будь‑яке мінімальне перевищення цього розміру треба вважати як підставу зарахувати такий предмет до великих. Якою б мінімальною не була різниця, нехай навіть в одну мільйонну від сантиметра, ми все одно зарахуємо предмет із таким розміром до великих. У такому разі не повинно сприйматися як щось парадоксальне те, що між 1 000 000 і 1 000 000,0000001 надзвичайно мала різниця, і предмет із першим із цих розмірів ми зарахували до невеликих, а предмет із другим розміром – до малих.
Отже, спірні випадки можуть з’явитися внаслідок двох причин: 1) кожен установлює межу самостійно (хоч, переважно – за подібними критеріями, що й інші) – як було зазначено, цього уникнути неможливо, тобто це можна лише врахувати, для прикладу, засобами паранесуперечливої логіки; 2) розмір предмета відповідає межі (такі спірні випадки легко долати, заокруглюючи до найближчого числа, яке належить або діапазонові невеликих розмірів, або діапазонові великих розмірів). Якщо ж низька точність порівнювання, виконуваного за допомогою тільки органів відчуття нас не задовольняє, то треба скористатися приладами. Водночас ніхто не буде використовувати для сортування огірків за їхніми лінійними розмірами електронного мікроскопа – у кожній практичній задачі, для якої виконують оцінювання «великий чи невеликий розмір», є свій достатній рівень точності.
Щодо встановлення меж може постати також таке питання. Нехай суб’єкт порівнювання лінійних розмірів сформулював свій розв’язок так: предмет S є високим порівняно з предметом Р. Наскільки коректною є така резолюція, якщо висота цих предметів становить по декілька метрів, а відмінність між розмірами – один міліметр. Наведене порівняння може мати сенс лише в такому контексті. Якщо, скажімо, з-посеред якоїсь етнічної спільноти низькорослих узяти когось, хто не є низьким (тобто середнього або високого), то він може виявитися низьким порівняно з членами іншої більш високорослої етнічної спільноти. Мірою під час такого порівнювання може бути якраз та різниця, яка є між високими й низькими в цій спільноті (розмір у межах між Δmax і Δmin для цієї спільноти низькорослих, див. рис. 1). Ми порівнюємо низькорослого з особами іншої спільноти (вищого зросту) за тими ж мірками, які є серед низькорослих. Якщо (Δmax – Δmin) > 1 мм, то оцінка одного як такого, що має велику висоту (тобто високого) порівняно з іншим, є некоректною.
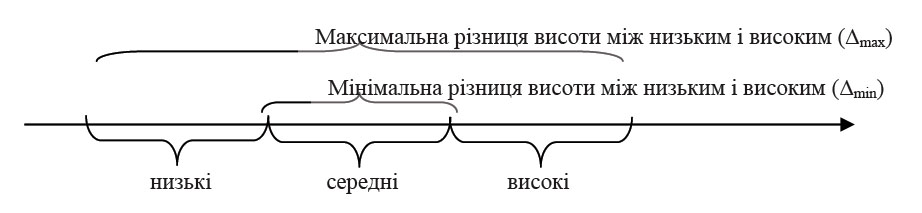
Рис. 1. Установлення міри для оцінювання одного предмета як великого порівняно з іншим
На підставі викладеного вище, можна стверджувати, що кожному оцінюванню певного предмета як великого, невеликого, малого, середнього, передує встановлення меж між цими діапазонами розмірів. Кожен буде встановлювати ці межі на підставі однакових принципів, оцінювати розміри за приблизно такою ж шкалою і тому оцінка у різних людей однакового предмета (як великого чи невеликого) з певним ступенем точності буде збігатися. У разі, коли важливо, щоб оцінки предметів як великих чи невеликих, отримувані кожним із певної групи суб’єктів максимально збігалися, залагоджують консенсусно, домовляючись щодо меж діапазонів неясних предикатів.
Ці міркування є чинними для всіх предикатів із семантикою кількісної невизначеності, які належать до першого типу предикатів із семантикою неясності, і до предиката «лисий» також.
Будь-яке оцінювання кількості виконують із певним ступенем точності. Коли ми кажемо лисий, лисуватий тощо, то також виконуємо оцінювання густини волосся. (Це оцінювання можемо виконати як обраховуючи, так і приблизно, тобто з певним рівнем точності вимірювання).
Для приблизного оцінювання кількості волосся треба насамперед установити шкалу діапазонів кількості волосся, наприклад: лисий (без жодної волосини) – має кілька волосків (практично лисий) – лисуватий (дуже розріджене волосся) – має залисину тощо (для цього може слугувати знана фахівцям шкала Норвуда). Тоді, на підставі такого шкалювання візуально оцінюють волосяний покрив, тобто відсоток голови без волосся. Це, у кожному конкретному випадкові, може залежати від довжини, товщини, кількості, кольору, розташування решток волосся на голові.
Наші оцінювальні дії в цьому разі нічим не відрізняються від пізнавальних дій у разі сортування огірків. Тож ми обов’язково встановлюємо межі, у тому числі між лисим і нелисим, а в такому разі сористичний парадокс можна виявити формальними засобами.
Подібні міркування стосуються також якісної неясності, наприклад, у разі оцінювання якогось предмета, як, скажімо, червоного. Коли ми поступово, покроково зменшуємо довжину хвилі електромагнетного променювання, то отримувані відтінки співставляємо з еталоном, а не з проявом ознаки на попередньому кроці, до того ж, якщо зміна кольору менша від порогу сприйняття людини. На певному етапі, коли кількість змін кольору стала помітною, то порівнюють цей колір з кольором еталона, який є у вигляді предмета з таким кольором (наприклад, колір пелюсток маку, чи крови), чи в атласі зразків кольорів. Отже й у цьому разі ми використовуємо орієнтир. Якщо є розбіжність в оцінюванні кольорів різними людьми (якщо хтось віднесе певний відтінок до помаранчевого тону, а хтось інший – до червоного), то в такому разі, як і в разі з розмірами, треба застосувати паранесуперечливу логіку.
Водночас, як і в разі кількісно невизначених предикатів, практика вживання назв кольорів ґрунтується на встановленні меж шляхом оцінювання того, до середнього відтінку якого кольору ближчим є ідентифікований колір.
У загальному випадку можливі два підходи до встановлення меж у контексті неясних предикатів. Є ситуації (як скажімо в разі семантики слова «великий»), коли потрібно мати змогу встановлювати різні межі відповідно до особливостей кожного конкретного випадку вживання неясного предиката. Воднораз є випадки, коли доцільно мати загальну значину межі, якщо цього вимагає потреба зоднаковлення людської практики. Для прикладу, в одній із царин діяльності для неясного предиката «молодь» встановлено чіткі межі: у Законі України «Про сприяння соціальному становленню та розвитку молоді в Україні», однозначно встановлено діапазон віку для молоді (від 14 до 35 років). У цьому разі внаслідок закріплювання чітких меж неясне поняття перетворили на ясне, надавши чітких меж. Воднораз в інших царинах діяльності предикат «молодь» залишається неясним. Отже, там, де потрібна зоднаковленість, де важлива узгодженість, як це є у згаданому законі щодо молоді, потрібно досягати консенсусу щодо меж. А там, де важливо мати можливість щоразу індивідуально підходити до встановлення меж, жодне зоднаковлення неприпустиме.
Повернімося до встановлення меж у разі неясного предиката «купа». Відзначимо головні постулати, які будуть підставами під час розв’язування цієї проблеми:
1. Купа, як нагромадження предметів, є відхиленням від площинності (якщо купа розташована на пласкій поверхні). Якщо ж купа розташована на поверхні довільної форми, то вона (купа) також буде площинним відхиленням від того закону зміни форми рельєфу, який був би без його спотворення купою.
2. Окрім умови, що купа має бути нагромадженням (тобто це не один шар предметів, а на нижньому прошарку повинні розташовуватися інші, принаймні ще один прошарок), доцільно використовувати як умову ідентифікування сукупу предметів як купи також наявність певного критерію форми цього нагромадження. Ба більше, умова наявності критерію форми, наприклад як кута бічної поверхні фігури згромадження (він може бути в межах від певної кількості градусів до 90 градусів), буде гарантією того, що сукуп предметів зібрано в більш, ніж один прошарок.
3. Купи, сформовані з елементів різної природи, відрізняються формою. Кути природного схилу (максимальний кут між основою і схилом насипу, за якого складники конусної купи не ковзають по поверхні, скочуючись донизу) для зернових мас різних культур коливаються в межах від 20-ти до 54-ох градусів. Для різних неорганічних матеріялів цей кут може сягати 90 градусів. Скажімо, помірно зволожений пісок має кут природного схилу 90 градусів, що потверджує піскова (пляжна) архітектура, у якій стіни моделей будівель, виготовлених з піску, мають саме такий кут. Водночас надмірно зволожений пісок, у якому рідина роз’єднує частинки, нівелюючи ефекти їхнього притягання, має мінімальні значини кута природного схилу.
4. Якщо кут між бічною поверхнею згромадження і горизонталлю є меншим від кута природного схилу (тобто біля основи конуса є гостріший кут), то це також буде купа, однак не з максимально можливим ступенем згромаджености. Лише за певного меншання цього кута можна твердити про межу між купою і некупою. Тому важливо з’ясувати, чи може бути якийсь природний критерій, який дасть змогу узгодити встановлення мінімального кута бокових поверхонь згромадження, які доцільно взяти як межу між купою і некупою.
5. Для встановлення межі переходу від купи до некупи потрібно з’ясувати, яким є мінімальний кут схилу біля основи конуса. Крім того, важливо, щоб зразковий критерій міг бути застосованим подібно до того, як застосовують зразки кольору, зафіксовані в дефініціях у тлумачних словниках. Тобто процедура має передбачати виконання її без допомоги якихось приладів. У певних випадках простіше оцінити відношення висоти купи до її діаметра чи радіуса (яке однозначно відповідає куту, незалежно від абсолютних розмірів купи), аніж розмір кута біля основи, що важливо для формування практично застосовного критерію купи.
6. Мінімальні значи́ни кута природного схилу мають: насичений водою пісок (рис. 2 а) і волога глина – 15° (за даними зі статті «Angle of repose» з Вікіпедії), – а також: масні глини – 12°–20°; гравій 10°–15°, торф без коріння 10°–15° (за даними зі статті «Кут природного укосу « з Вікіпедії).
7. Оскільки встановити відношення лінійних розмірів легше, аніж розпізнавати скільки градусів є в куті, то за основу доцільно брати не кількість градусів, виражену цілим натуральним числом (у сенсі, що кількість мінут і секунд дорівнюватиме нулю), а виражене цілим числом відношення висоти h до радіуса основи r купи у формі конуса (рис. 2 б). Близьким до кута 15° є відношення h/r = 1/4 = 0,25; близькі до цього відношення виражені цілим числом кути 14° і 15°: tg (14°) = 0.24933, а tg (15°) = 0.26795. Близьким до кута 12° є відношення h/r = 1/5 = 0,2; близькі до цього відношення виражені цілим числом кути 11° і 12°: tg (11°) = 0.19438, а tg (12°) = 0.21256.

Рис. 2 а – форма купи піску, насиченого водою; б – геометрична модель мінімальної купи в разі співвідношення h/r = 1/4
На підставі виконаного дослідження можна зробити такі висновки. У процесі діяльності нам потрібно мати слова без вказівки якісних чи кількісних меж для тих випадків, коли в кожній конкретній ситуації потрібно встановлювати свою межу. Відсутність універсальної межі не означає, що межу для кожного конкретного випадку не встановлюють, або що її неможливо знати. Установлювання меж неясних понять є умовою їхнього вживання на позначення тих чи тих об’єктів дійсності. Водночас, для уникнення сористичних парадоксів, доцільно закцентувати в дефініціях предикатів із неясною семантикою, що вони набувають ясності шляхом встановлення меж у кожному конкретному випадку застосування (або індивідуальним установленням таких меж, або внаслідок досягнання консенсусу). Поняття «купа» можна здефініювати, узявши за основу мінімальний кут природного схилу, чи цілочисельне відношення радіуса основи фігури купи до її висоти, близьке до згаданого мінімального кута природного схилу.